Decimals are an alternative way of representing a port of whole number.

Decimal are numbers that are used in situations where more accuracy is required than the whole number can provide. For instance, when weighing a weight of bag of potato on the weighing machine, we do not always find the weight equal to a whole number on the scale.

Terms used when working with decimals:

·         Terminating decimals -  decimals have a certain number of decimal places.

For example:

0.34, 4.125, 3.2

·         Recurring decimals – decimals have a digit or digits that keep repeating.

For example:

   = 0.333333 …... the 3 is repeated.

 = 0.166666 …... the 6 is repeated.

   = 0.131313 ……. the 13 is repeated.

The decimal can also be represented on a number line.

Life example of integers in business

https://medium.com/a-distant-read/grocery-shopping-in-madang-9139f362e116

The green bunch of banana is selling for K10.00 at the Madang market.

In decimal calculation we have to understand the place value of decimals chart, changing between fractions and decimals, rounding decimals, adding and subtraction decimals also multiplying and dividing decimals.

Place value decimal chart

 

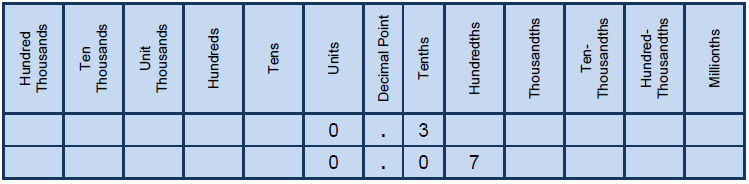
The decimal 0.3 in the chart is often said to as ‘point three’ or ‘zero point three and also be said as three tenths because it reflects the place value of the number.

The other decimal 0.7 in the chart is often said as ‘point zero seven or zero point zero seven and also said seven hundredths.

 Changing between decimals to fractions

The decimal can be changed from decimal to fractions or vice-versa. Using the place value of decimals, it is easy to change decimals to fractions.

From the place value decimal chart we know that 0.3 =  and 0.07 =  .

The table shows decimals represented as fractions

 

Decimal	Fraction
0.05	0.05 =
0.001	0.001 =
0.49	0.49 =
0.65	0.65 =  =
-0.44	-0.44 =  =
2.75	2.75 =  =
3.87	3.87 =

 

Changing fractions to decimals

The fractions can be changed from fractions to decimals using two methods.

Method 1:

The first method uses the place value of decimals i.e: tenths, hundredths, thousands, etc. This method is a quick way of changing from a fraction to a decimal but is limited in what fraction for.

For example:

Take a look at the fractions. If the fractions have a denominator of 10, 100, 100 or if an equivalent fraction has a denominator of 10, 100, 100 it can be written as the decimal equivalent.

·         The decimal three tenth, as a decimal this is 3 in the tenths place value.

  = 0.3

·         Two fifths is equivalent to four tenths as a decimal this is a 4 in the tenth place.

  =   = 0.4

 

·         Three quarters is equivalent to seventy-five hundredths, as a decimal this is 70

hundredths or 7 tenths and 5 hundredths.

  =   = 0.75

 

·         Three twentieths is equivalent to fifteen hundredths, as a decimal this is 10 hundredths or 1 tenth and 5 hundredths.

  =   = 0.15

 

Method 2

The second method is suitable for long division or use of calculator.

For example:

1.        This is calculated 3  5 = 0.6

 

2.       This calculated as 4  9 =

 

3.       This is calculated as 2  7 = 0.28571

Using your scientific calculator to find the decimal of a fraction

 

 

Rounding Decimals

Round of decimals is an important to express a decimal value to significant value. In rounding a decimal, a place value or a specified number of decimal places to which the number must be rounded will be stated.

For example:

Round 0.3292 to the nearest hundredth.

The number 0.3292 is, in size, between 0.32 and 0.33 when the hundredth when the hundredths place or 2 decimal place is being considered. The purpose of rounding is to say that 0.3292 is closer to 0.32 than 0.33.

There are two steps to round to a stated place value.

Step 1: Locate the digit in the place value being stated and underline it.

0.3292

 

Step 2: Locate the digit to the right of the place value stated. Now circle this digit.

0.32 2

If this digit is ‘less than 5’ then the digit in the stated place value stays the same.

If this digit is ‘5 or more’ then the digit in the stated place value increases

 

by one.

As the digit is the 2 will increase to 3.

The answer is 0.3292 ≈ 0.33.

 

Addition and subtraction of decimals

In addition, or subtraction of decimals, the number of the same place value must be line up before the operation can be performed.  To achieve this, the numbers are placed vertically. If a whole number is part of the question, then the decimal point goes to the right of the units’ place value.

For example,

Add the decimal 9.27, 3.6 and 12

To carryout out addition of decimals, arrange numbers vertically, lining up numbers of the same place value and adding zeros to obtain the same number of decimal places.

·         Add the numbers in the hundredths column (=7), put the 7 in the hundredths column.

·         Add the numbers in the tenths column (=8), put the 8 in the tenths column.

·         Add the numbers in the units column (=14), put the 4 is the units column, and the carry in the tens column.

·         Add the numbers in the tens column and the carry (=2), put the 2 in the tens column

¹9.27

3.60

      +    12.00

              24.87

    Using the scientific calculator

 

For example,

11.346 take 7.32.

Arrange numbers vertically, lining up numbers of the same place value and adding zeros to obtain the same number of decimal places.

 

·         In the thousandths column, 6-0=6

·         In the hundredths column, 4-2=2

·         In the tenths column, 3-3=0

·         In the units column, 1-7 cannot be done, so borrow 1 from the next column and pay back 10. Now 11-7=4

¹11. 346

                  -7. 320

     4.026

    In using a scientific calculator

   .

 

Multiplication of decimals

In multiplication of decimals by 10, 100, 1000 etc. is slightly different to whole numbers because of the presence of the decimal point. This is achieved by moving the decimal point to the left by the number of places equal to the number of zeros. Moving the decimal point to the left decreases the size of the number, each place by a factor of 10.

For example:

a.       367.8 ÷ 100

100 contains zeros, so move the decimal point 2 places to the left.

101367.8 ÷ 100 = 3.67

 

b.      0.573 ÷ 1000

1000 contains 3 zeros, move the decimal point 3 places to the left.

0000.573 ÷ 1000 = 0.000573 Sometimes zero(s) need to be inserted.

       c. 50 contains 1 zero, move the decimal point 1 place to the left and then divide by 5.

           15.25 ÷10 = 1.525 then 1.525 ÷ 5 = 0.305

            Recall: a negative ÷ a positive = a negative

            Answer is −0.305

 

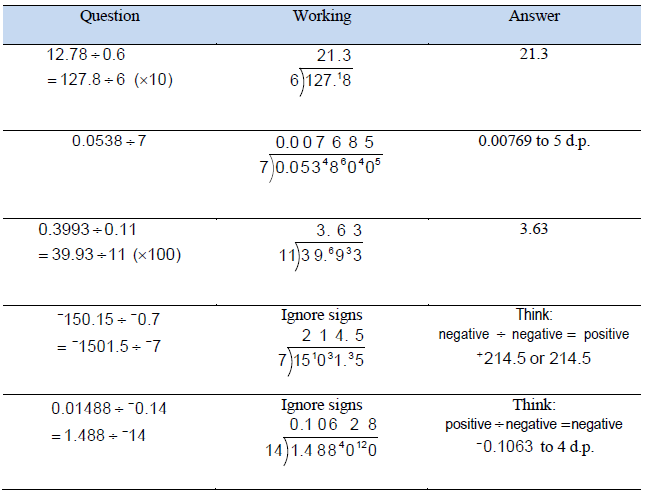
Division of decimals

 In dividing decimals, the divisor (number being divided by) should be a whole number. To        achieve this, the divisor must be multiplied by 10, 100, 1000 etc. to make the divisor a whole number. The dividend (number being divided into) also needs to be multiplied by 10,100, 1000.