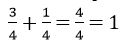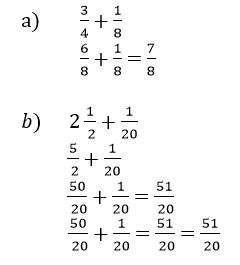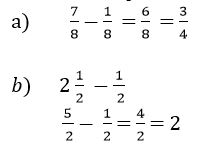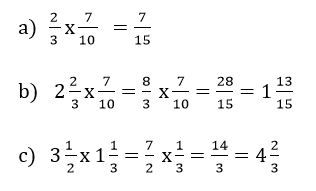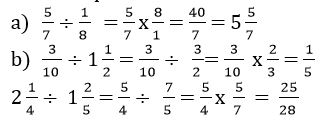Fractions are rational number which is expressed in the form where a and b are integers but b is not equal to zero.
In baking, fractions are useful to measure the different quantity of ingredients. In sports we use fractions to represent the half-time or break during the game. In building and construction, carpentry used fraction to find the length of each timber for building.
To understand problems in fraction we have to learn these terms.
· Fraction- A number that represents equal parts to a whole and has a numerator and denominator.
· Numerator -The part of a fraction above the line, which tells how many parts are being counted.
· Denominator- The part of a fraction below the line, which tells how many equal parts there are in the whole or in the group.
· Proper fraction - A fraction in which the numerator is less than the denominator
· Improper fraction- A fraction in which the numerator is greater than or equal to the denominator
· Mixed number- A whole number and a fraction
· A proper fraction has the number less than the denominator.
Example of fractions in cooking
In order to bake cookies, we need these following fraction of ingredients.
· ¾ cup butter
· 1 cup brown sugar
· ½cup sugar
· 1 egg
· ¼cup water
· 1 ½ table spoon vanilla
· 1 cup flour
· 1 table spoon of salt
· ½ tsp baking soda
· 2 ¾ cups of oats
Example of fractions in sports
In sports, half-time is used to represent the interval between the two half of the match. The following are some of the sports that used half-time.
· Australian rules – Two periods of 20 minutes plus stoppage time
· Basketball - 12 minutes each
· Netball - Two periods of 15 minutes each
· Rugby league – 40 minutes
· Rugby union – 40 minutes
In performing calculations with fractions we have to bear in mind some rules to help us when dealing with type of fractions.
Addition of Fractions
Rule 1: Same denominator
Fractions with the same the denominator.
1. Add the fractions. If the fractions are a combination of mixed and problem fraction convert the mixed fractions to improved fraction and add the fractions.
2. Simplify the fraction to proper fraction
For example:
a
Rule 2: Different denominator
Fractions with the different denominator.
1. Find the lowest common denominator
2. Add the fraction. If the fractions are a combination of mixed and problem fraction convert the mixed to improved fraction and add the fractions.
3. Simply the fraction to proper fraction
For example:
Subtraction of Fractions
Rule 1. Same denominator
Fractions with the same denominator
1. Subtract the fractions. If the fractions are a combination of mixed and problem fraction convert the mixed fractions to improved fraction and subtract the fractions
2. Simplify the fraction to proper fraction
For example:
Rule 2: Different denominator
Fractions with different denominator
1. Find the lowest common denominator
2. Subtract the fractions. If the fractions are a combination of mixed and problem fraction convert the mixed to improved fraction and add the fractions.
3. Simplify the fraction to proper fraction
For example:
Multiplication of fractions
Rule:
· Express mixed numerals as improper fractions.
· Cancel common factors where possible.
· Multiply numerators and multiply denominators.
· When necessary express the result as a mixed numeral and check that fractions are reduced to their simplest form.
For example:
b)
Rule:
· Change the division sign to multiplication sign and invert the number to the right of the sign.
· Convert the mixed fraction to improper fraction.
· Multiply the numerators.
· Multiply the denominators.
· Simplify to proper fractions.
For example: